Modelling of Seismic Wave Propagation
When there is a major geological event, such as an earthquake, or a large volcanic eruption, seismic waves travel through the solid and liquid rock layers of the Earth’s surface (similar to when you feel the earth shaking when a heavy lorry or train passes nearby). These can be detected with scientific instruments, and the numerical modelling of seismic wave propagation is vital for identifying places where earthquakes are likely to originate from in the future, studying processes of preparation and origin of earthquakes, prediction of earthquake ground motion at a site of interest, forecasting of earthquake effects on buildings and structures, searching for oil, gas, coal, kaolin and other raw materials, estimating the hydraulic properties of rocks in hydrocarbon reservoirs, monitoring tsunami, monitoring volcanic eruptions, monitoring and locating nuclear explosions, and other seismological research and practical applications.
There is a variety of physical processes inside the Earth. The complexity of the processes is due to both the complicated rheology of the Earth’s material and the complicated spatial distribution of values of physical and chemical parameters in a large range of scales – from thousands of kilometres down to micrometres. For studying all these processes it is very important to know the seismic model and seismic wave propagation.
The unique physical properties of seismic waves are the reason why the static seismic model of the Earth’s interior (a model of a spatial distribution of physical parameters that determine seismic wave propagation) is the most accurate model of the interior of our planet, although we still do not know enough to fully understand important processes inside the planet.
What is numerical modelling of seismic wave propagation? Seismic wave propagation in an unbounded homogeneous perfectly elastic isotropic medium can be described by exact solutions. As it is already obvious, the Earth’s interior is dramatically heterogeneous. Exact solutions do not exist, it is necessary to apply approximate numerical methods.
A team of numerical modelling of seismic wave propagation and earthquake ground motion (Peter Moczo, Jozef Kristek, Miriam Kristeková, Martin Gális, Dávid Gregor) develop finite-difference (FD) methods of modelling that are sufficiently accurate and computationally efficient.
P. Moczo and J. Kristek were first to work with equations which have the same form at an interface and away from the interface – which is the basic condition for the heterogeneous FD schemes. They developed discrete grid representations of a continuous and discontinuous material heterogeneity in a perfectly elastic and viscoelastic continua, and recently also in a poroviscoelastic continuum. Thanks to these representations, the FD method of numerical modelling of seismic wave propagation and earthquake ground motion is computationally more efficient in the surface sedimentary structures (where the strongest anomalous earthquake motions and thus also big earthquake damage occur) than other numerical methods. Numerical modelling is computationally very demanding and it is impossible to investigate realistic models of the Earth without supercomputers. Supercomputer Aurel significantly helps.
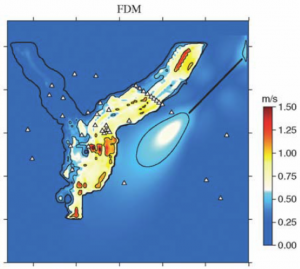
Prediction of the peak ground velocity of seismic motion at a free surface of the sediment-filled Alpine valley in Grenoble, France, based on numerical modelling of seismic motion due to a hypothetical earthquake on the Belledonne fault.