Prof. Roman Martoňák, the Department of Experimental Physics,
the Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava
When you spread a freshly ironed table cloth on the table, it is flat and plain. It seems natural that it does not ripple by itself. Is it possible for something flat to ripple itself? Not according to our ordinary experiences. However our experiences come from our contact with things that are similarly sized to us. Is it possible that in another world, for example the microworld of atoms, our experience is false and things work differently?
To find the answer, we need to turn to physics, which can also study the microworld. And it will surprise us: things can ripple by themselves as long as they are sufficiently thin. It is best when the material is so thin that it cannot be any thinner. What is the thinnest material we can imagine? Since all matter consists of atoms, the lowest thickness is one atom. It cannot be any thinner, since simply put “we cannot split an atom into two halves”. But can something like that – a membrane with the thickness of just one atom – even exist? Will it hold together if it is so thin? Can it be made, and if so, of what?
We already know that a material like this can exist and how to make it. And there is another surprise: it is quite simple to create. The first to do so were Russian scientists A. Geim and K. Novoselov, who used duct tape to tear away a one atom thick layer from graphite – pencil lead. They called the layer graphene, and so created the first sample of the two-dimensional material. It is two dimensional, because its thickness is much smaller than its width and length. For their discovery, which started a new era in physics and technology, they were awarded the Nobel Prize for physics in 2010. Graphene is considered very promising in electronics, due to its very interesting electrical properties.
Graphene has also other extraordinary properties, like its high mechanical strength and heat conductivity. Today graphene is no longer the only two-dimensional material, there are many others. A single atom thick layer of boron nitride BN is most similar to graphene, since boron and nitrogen are next to carbon in the periodic table, to the left and to the right. Apart from that, such layers can be made from other elements such as silicon, germanium, phosphorus, but also compounds like molybdenum disulphide MoS2 and the list of these materials keeps expanding. Furthermore different two-dimensional materials can be stacked on top of each other to create new materials with interesting properties and potential for use in all kinds of applications.
Let us go back to how a membrane such as graphene can ripple by itself. Physics teaches us that in the microworld there is constant movement. Atoms keep moving faster as the temperature increases. When we cool something down, it means we slow down the movement of the atoms, and warming up means increasing the speed of the atoms. This motion is the reason why graphene and other two dimensional materials cannot be completely flat and smooth, since to achieve that, we would have to stop the movement of the atoms completely. It seems almost possible when we lower the temperature a lot. And here comes another surprise – atoms cannot be completely stopped like a car or a tennis ball. Even if the thermal motion stopped completely, atoms would still not remain at the same position. This is caused by so called quantum mechanics, which says that even at the lowest temperature, the atoms would still perform some movement, also known as zero-point motion. Let us say that the atoms always shake at least a little. This quantum zero-point motion also creates ripples on graphene, and there is no way to stop it. As physicists, we would like to know the properties of these quantum ripples in graphene. They are however very hard to calculate, since quantum ripples are more complicated than thermal ones. And that is where the Aurel supercomputer steps in to help.
In 2013 Juraj Hašík, a student of theoretical physics at the Faculty of Mathematics, Physics and Informatics of Comenius University in Bratislava, started to tackle the problem under the supervision of Prof. Roman Martoňák. As a part of his masters thesis he wrote a code that can simulate quantum ripples in graphene mathematically. However the quantum world is complicated, and the computation needs to perform a huge number of mathematical operations. If it were run it on a normal personal computer, it would take many years. Thankfully Aurel is a parallel computer and can perform many (tens, hundreds, even thousands) computations at the same time. A big problem is split into small parts which can be solved separately and the whole is solved much faster. Writing such a program is not easy of course, but it is worth the effort. Juraj Hašík continued his research after he left to join a PhD programme at the International School for Advanced Studies, Trieste, where he also worked with Prof. Erio Tosatti.
What did Aurel tell us about the quantum ripples in graphene? It turned out that they are completely different from the classical ones. Over longer distances they are weaker, and so graphene stays flat. Over shorter distances they are stronger, making graphene more rough. Simply put, quantum graphene at lower temperatures is both flatter and rougher than the classical one. A scientific article about the structure of quantum graphene was published on 4 April 2018 in the journal Physical Review B in the section Rapid Communications, which publishes short articles presenting highly original and significant results in the area of condensed matter physics.
The paper was also highlighted by the editors as the Editors’ suggestion.
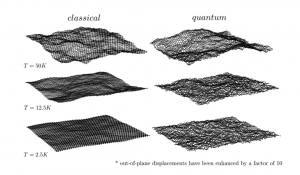
Rippled graphene from classical (left) and quantum (right) simulations at the temperatures 50 K (top), 12.5 K (center) and 2.5 K (bottom). Displacements in the vertical direction are amplified tenfold for better visualization.
